3. Физика процесса.
Оказалось, что неравновесные процессы, происходящие в КС таких аппаратов чрезвычайно сложны, кроме обмена импульсом и теплообменом между паровым потоком и частицами жидкой фазы протекают фазовые переходы. В КС осуществляется дробление и разгон частиц жидкой фазы, а также почти полная конденсация паровой фазы на более холодной жидкости, что приводит к перестройке структуры потока. Если в начальном участке КС движутся разделенные, но взаимодействующие паровая и жидкая фазы, то затем поток приобретает капельную структуру с практически равномерно распределенными по объему каплями.
Т.к. струя дробится на мелкие капли, то в результате площадь поверхности теплообмена оказывается очень большой, при этом теплообмен на струе жидкости становится интенсивным.
В конце КС, структура потока перестраивается, среда приобретает пенную, тонкопленочную структуру с заполненными паром полостями, которая характеризуется максимальной площадью поверхности контакта фаз. Это соответствует максимальной интенсивности теплообмена, конденсации пара и соответственно возрастанию плотности смеси [1]. При конденсации пара создается разряжение, т.к. конденсат имеет значительно меньший удельный объем.
На выходе из КС, когда паровая фаза в основном сконденсировалась, поток через пенную структуру переходит в пузырьковую (пузырьки пара в жидкой среде). Такая среда обладает необычными свойствами, по отношению к скорости распространения звука в ней, что и составляет основу для формирования скачка давления.
Рассмотрим историю этого вопроса. В работах к.т.н. Н.Г. Морозова (ВТИ) [2] впервые детально исследовавшего распределение давления по длине проточной части струйных аппаратов при различных режимах работы, еще в 1939-1940г. было предложено объяснение наблюдающегося в диффузоре этих аппаратов скачка давления. Это объяснение основывалось на рассмотрении смеси жидкости с не сконденсировавшимся паром как квазиоднородной эмульсии, к которой приложимы все обычно применяющиеся уравнения движения однородной сжимаемой жидкости, а также понятия о критической скорости, критическом расходе и пр. Н.Г. Морозовым было дано общее уравнение движения такой эмульсии, учитывающее как трение, так и конденсацию (или испарение) и изменение секундной массы струи. Скачок давления в диффузоре объяснялся им как скачок уплотнения, сопровождающий переход от сверхзвуковой скорости струи к дозвуковой с завершением при этом конденсации пара, а величина скачка давления определялась с помощью уравнения количества движения.
Основанием для развития теории такого рода аппаратов стали работы по изучению скорости звука в парожидкостных и газожидкостных смесях. Так в работе [3] было теоретически показано, что процесс кавитации (появление в жидкости зародышей паровой фазы) сопровождается резким уменьшением величины скорости звука.
В работе [4] были рассчитаны значения скорости звука для разных температур жидкости в насыщенной воде со стороны двухфазной области, при этом было обращено внимание на аномально низкую скорость звука в такой среде.
В работе [5] как теоретически, так и экспериментально было показано, что скорость звука в газожидкостной смеси в большой степени зависят от сжимаемости этих компонент. Смесь, состоящая из почти несжимаемой жидкости и сжимаемого газа или пара, имеет более высокую сжимаемость, чем даже у газовой фазы, а потому звуковая скорость в ней ниже, чем просто в газе.
Итак, скорость звука в средах аналогично той, что мы имеем на выходе из КС (гомогенная пузырьковая смесь газ — или пар — жидкость) имеет аномально низкое значение скорости звука (рис. 4.1., 4.2.)

Значение скорости звука в такой среде может опускаться, например, до 10 м/с (скорость звука просто в паре или в воде соответственно порядка 500 или 1500 м/c). Таким образом, при умеренных скоростях 40 — 50 м/c движения парожидкостного потока мы можем получить сверхзвуковое течение по отношению к этой аномально низкой скорости звука.
Итак, на выходе из КС мы можем с малыми энергозатратами получить сверхзвуковую скорость.
Затем сверхзвуковой поток переходит из КС в ГД (рис.2), т.е. в канал постоянного сечения. Учитывая, что скорость смеси достаточно велика при относительно небольшой длине канала, то процесс, происходящий в нем можно считать адиабатным.
При торможении потока в адиабатном канале, согласно формуле Эддингтона, из работы [6], для газожидкостной смеси интенсивность скачка давления равна числу Маха в квадрате
Р2/Р1= М2,
где Р1 и Р2 — соответственно давления до и после скачка.
Число Маха дает отношение скорости потока W к скорости звука в потоке. С:
М = W / C
Так, если W= 50 м/с, С=10м/с, то М=50/10=5, тогда Р1 / Р2 = 52 = 25, т.е. имеем двадцатипятикратный (!) скачок давления. С учетом падения давления пара в сопле и перед скачком давления смеси, все равно давление после скачка может существенно превышать его значение на входах в аппарат.
Как показали визуальные наблюдения, выполненные на аппаратах с КС и ГД из кварцевого стекла, за скачком поток имеет однородную структуру (жидкость практически лишена паровых пузырьков и поэтому оптически прозрачна), т.е. переход через скорость звука сопровождается скачком давления с “захлопыванием” пузырьков и полной конденсацией пара.
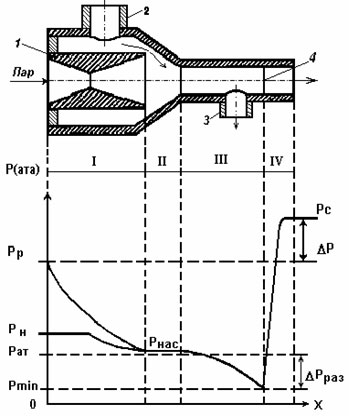
Статическое давление по длине аппарата ведет себя следующим образом:
I — на этом участке давление падает в паровом и жидкостном соплах;
II — на срезе сопла давление примерно равно давлению в КС, если сопло работает в расчетном режиме. Давление в КС по завершению формирования смеси устанавливается равным давлению насыщения при температуре на границе раздела фаз, в зависимости от требуемой температуры смеси оно может быть больше или меньше атмосферного;
III — давление в начале ГД падает перед скачком, т.к. сконденсировавшийся пар занимает меньший удельный объем, чем до конденсации, а сечение цилиндрического участка постоянно в отличии от КС ;
IV — дозвуковое течение смеси. На границе участков III и IV происходит скачок давления, его рост продолжается в диффузоре.
Рраз — разряжение в ГД, Р- превышение давления смеси на выходе из аппарата над давлением пара на входе.
 Larisa (12 Декабрь 2016 - 14:42) писал:
Larisa (12 Декабрь 2016 - 14:42) писал:














